
Proper Motions
According to SIMBAD, the proper motion in right ascension direction (east/west) for Alkaid is -121.17 mas/yr. Its proper motion in declination direction (north/south) is -14.91 mas/yr. And, its radial velocity is -10.9 km/sec.
To find the tangential velocity for Alkaid, we must first use the formula μ = √Ra ² + Dec ², where μ = proper motion, Ra = right ascension and Dec = declination.
μ =
Ra = -121.17 mas/yr
Dec = -14.91 mas/yr
μ = √Ra ² + Dec ²
μ = √121.17 mas/yr² + -14.91 mas/yr² = 121.92 mas/yr
Next, we must convert mas/yr into km/sec. To convert we divide by 1000.
(121.92 mas/yr)/1000 = .12192 km/sec
Then, we use the formula Vt = μ(4.74d), where distance = 31.87 parsec (found in the angles in parallax lab above.
Vt =
μ = .12192 km/sec
d =31.87 parsec
Vt = μ(4.74d)
Vt = 2192 km/sec (4.74 x 31.87 parsec) = 18.44 km/sec
Now, we can use our tangential velocity of 18.44 km/sec to find the space velocity for Alkaid. To do this we use the formula Vs = √Vr² + Vt².
Vs =
Vr (from SIMBAD) = -10.9 km/sec
Vt = 18.44 km/sec
Vs = √Vr² + Vt².
Vs = √-10.9 km/sec ² + 18.44 km/sec ² = 21.42 km/sec
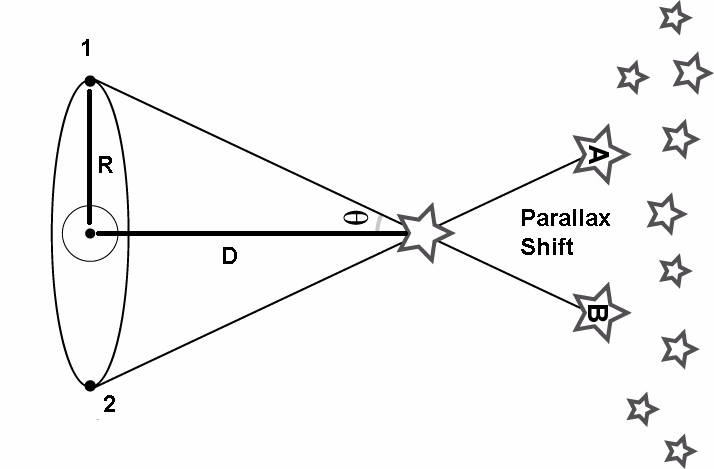
Angles and Parallax
According to SIMBAD, the parallax angle for Alkaid (spelled Alcaid in SIMBAD) is 31.38 mas.
In order to convert this to arc seconds, you must divide the milliarcsecond by 1000.
31.38 mas/1000 = .03138 arcsec
Now, to find distance you use the formula distance (parsec)= 1/ parallax angle (arcsec)
1/.03138 arcsec = 31.87 parsec
Math


